Conjuntos.

Cualquier colección de objetos o individuos se denomina conjunto. En el contexto de la matemática, el término conjunto no tiene una definición sino que es un concepto.
Un conjunto está integrado por objetos y los objetos que integran el conjunto se llaman elementos de ese conjunto.
En general usaremos letras mayúsculas para designar a los conjuntos y letras minúsculas para designar a sus elementos. Si a es un elemento del conjunto A se escribe a ∈ A y se lee a pertenece a A. Si a no es elemento del conjunto A se escribe a A y se lee a no pertenece a A.

¿Cómo lo definimos?.

Definir un conjunto es describir de una manera precisa, sin ambigüedades, cuáles son los elementos de dicho conjunto. Existen distintas maneras de definir un conjunto. Por extensión, es decir listando todos los elementos del conjunto separados por comas y encerrando todo entre llaves:
A = {1, 2, 3, 5, π}.
El orden en el cual se enumeran los elementos del conjunto es irrelevante, y además se consideran una sola vez.
Por ejemplo: {1, 2, 3}, {3, 2, 1} y {1, 1, 2, 2, 2, 3} describen al mismo conjunto.
Otra forma de describir un conjunto es por comprensión, es decir enunciando una propiedad de los elementos que lo integran. A = {x | x cumple la propiedad P }, que se lee: “el conjunto de los x tales que x cumple la propiedad P”.

Diagramas de Venn.

Es frecuente utilizar ciertos diagramas, llamados diagramas de Venn, para representar a los conjuntos. Un conjunto se representa con una línea curva cerrada, y sus elementos con puntos en el interior. Por ejemplo, el diagrama de Venn para el conjunto A = {a, b, c, d} es:

Subconjuntos.

Consideremos los conjuntos A = {1, 3, 5} y B = {1, 2, 3, 4, 5}.
Como podemos ver, los elementos de A: 1, 3 y 5, también son elementos de B. Decimos entonces que A es un subconjunto de B, o que A está incluido en B.
Un conjunto A es un subconjunto del conjunto B si todo elemento de A es también elemento de B. Se denota A ⊆ B y se dice que A está incluido o contenido en B.
En particular, todo conjunto está incluído en sí mismo. Por ejemplo: A = {1, 3, 5} está incluido en A, y lo escribimos A ⊆ A.
Dos conjuntos A y B son iguales si los elementos de A son elementos de B, y viceversa. Es decir, si A ⊆ B y también B ⊆ A.
Notemos que dos conjuntos pueden ser distintos pero tener uno o más elementos en común. Por ejemplo. A = {2, 4} y B = {1, 4, 6} son distintos pero el 4 es un elemento de ambos conjuntos.

Conjuntos disjuntos.

Dos conjuntos se dicen disjuntos si no tienen ningún elemento en común. Los conjuntos C = {2, 4, 6} y D = {1, 3, 5, 7} son disjuntos.
Si A es un subconjunto de B, pero distinto de B, se dice que A es un subconjunto propio de B. La notación A ⊆ B es correcta, pero si queremos resaltar que A y B son distintos, escribimos A ⊂ B.
Consideremos los conjuntos A = {x | x es un natural par y x < 10}, y B = {2, 4, 6, 8, 10}. En este caso, todo elemento de A es un elemento de B, y por lo tanto A es un subconjunto de B: A ⊆ B. Además se cumple que 10 pertenece a B pero no pertenece a A, por lo cual A y B no son los mismos conjuntos. Decimos entonces que A es un subconjunto propio de B y lo escribimos A ⊂ B.

Intervalos de números reales.

Un intervalo de números reales es un subconjunto de R que tiene la siguiente propiedad: dados dos números a y b en el intervalo, todos los números comprendidos entre a y b también pertenecen al intervalo.
Gráficamente, un intervalo se identifica en la recta real con un segmento o una semirrecta, con o sin sus extremos, o con toda la recta real.
Por ejemplo:. el conjunto {x | 2 ≤ x ≤ 8} es un intervalo, que se representa en la recta real como un segmento con extremos 2 y 8.
El conjunto {x | x > −5} es un intervalo, que se representa en la recta real como una semirrecta, con origen en -5, sin contar este extremo.
Para los intervalos se utiliza una notación específica, y se los clasifica además en intervalos cerrados [ ], abiertos ( ) y semiabiertos [ ) ó ( ].

Conjunto Universal y Conjunto Vacío.

No necesariamente los elementos de un conjunto son de la misma naturaleza, por ejemplo, el conjunto C formado por los estudiantes de sexto y el número π es válido como conjunto. Sin embargo, es muy poco interesante en la teoría. En general nos referiremos a conjuntos cuyos elementos tienen una propiedad en común.
Por ejemplo: A = {x | x es un natural impar}, B = {x | x es un natural mayor que 9} y C = {x | x es un natural menor que 35}, son conjuntos cuyos elementos son números naturales.
En el caso anterior los conjuntos A, B y C son subconjuntos de N, y podemos considerar a N como conjunto universal: U = N. Notemos que A, B y C son también subconjuntos del conjunto Z de números enteros, por lo que también podría fijarse U = Z. Por ello siempre debe dejarse expresado explícitamente el conjunto universal que se desee considerar.
En un diagrama de Venn el conjunto universal se representa con un rectángulo y el conjunto que nos interesa representar, digamos A, se denota con una curva cerrada dentro del rectángulo.

 

Un conjunto que no tiene elementos es llamado conjunto vacío o conjunto nulo lo que denotamos por el símbolo ∅.
Por ejemplo:
Sean A = { 2, 4, 6 } y B = { 1, 3, 5, 7 } encontrar el conjunto de los elementos iguales entre A y B. El resultado muestra que no hay elementos entre las llaves, si este es el caso se le llamará conjunto vacío ó nulo y se puede representar como:

 

Operaciones entre conjuntos.

Así como pueden definirse diversas operaciones entre números, también existen operaciones entre conjuntos. El resultado de una operación entre conjuntos es a su vez un conjunto.
Fijemos un conjunto universal U y consideremos todos los subconjuntos de U. Entre estos conjuntos están definidas las operaciones de unión, intersección y diferencia. Además, para cada conjunto se define el complemento. El resultado de cada una de estas operaciones es un subconjunto de U.

Unión de conjuntos.

Sean A y B dos conjuntos. Se llama unión de A y B, y se escribe A ∪ B, a un nuevo conjunto cuyos elementos pertenecen a A o a B.
Por comprensión, la unión entre los conjuntos A y B se define así:
A ∪ B = {x/x ∈A ∨ x ∈B}
En particular, A y B son subconjuntos de A ∪ B, pues todos los elementos de A y todos los elementos de B pertenecen a A ∪ B.
En un diagrama de Venn representamos la unión de dos conjuntos sombreando el área que cubren ambos conjuntos:

 

Intersección de conjuntos.

Sean A y B dos conjuntos. La intersección A ∩ B entre A y B es el conjunto cuyos elementos pertenecen a A y pertenecen a B.
Por comprensión, la intersección de los conjuntos A y B se define como:
A ∩ B = { x | x ∈ A y x ∈ B}
En un diagrama de Venn la intersección de dos conjuntos se representa por la región que está determinada por el interior de las curvas cerradas que determinan los conjuntos. Esta región se la destaca con un sombreado. Obsérvese que la intersección de dos conjuntos es vacía si y sólo si no hay elementos comunes entre ellos. Esto se grafica con dos curvas cerradas que no se cortan.

 

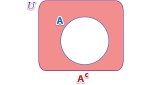
Complemento de un conjunto.

Fijemos U un conjunto universal y A un subconjunto de U. El complemento de A con respecto a U es el conjunto cuyos elementos son todos los elementos de U que no pertenecen a A.
En un diagrama de Venn el complemento de A es la región exterior de la curva cerrada que determina A. Lo destacamos con un subrayado o sombreado.

Diferencia de conjuntos.

Sean A y B dos conjuntos. La diferencia o complemento relativo A − B entre A y B es el conjunto de todos los elementos que pertenecen a A y no pertenecen a B.
En un diagrama de Venn representamos la diferencia entre los conjuntos A y B, destacando la región que es interior a A y exterior a B.

 

El conjunto A diferencia simétrica B, escrito A Δ B, está formado por elementos del universo que pertenecen o bien a A o bien a B pero no a ambos al mismo tiempo, es decir los elementos no comunes entre A y B, se podría decir que la diferencia simétrica es la operación complementaria (contraria) a la intersección.

 
En este link pueden bajar el apunte de esta unidad, nos vemos en el aula!!!!!

Aquí tienen la Guía de Trabajos Prácticos para trabajar en el aula y las tareas